미누에요
[자료구조] 최소비용 신장트리(MST), Prim 알고리즘 본문
최소비용 신장트리(MST, Minimum Spanning Tree)
- 가중치 그래프에서, 간선들의 비용 합이 최소가 되는 신장트리
최소비용 신장트리는 그래프가 아니라 트리 이기때문에 사이클이 구성되지 않아야한다.
우선, 최소비용 신장트리가 아니라 일반적인 신장 트리의 모습이 아래에 있다.

위 그림처럼 그래프에서 나올 수 있는 신장트리는 여러 개일 수 있다.
하지만, 일반적인 신장트리와 다르게 최소비용 신장트리는 간선에 가중치가 있기때문에, 그 값에 따라 최소한의 비용으로 나타낼 수 있는 트리여야 한다.

위 사진처럼 각 간선에 가중치가 있고, 그 가중치가 가장 작은 간선으로 이동하는 방식으로 얻은 트리가 최소비용 신장트리, MST이다.
최소비용 신장트리(MST)를 구하는 방법에는 크게 Prim 방법과 Kruskal 방법이 있다.
Prim 방법
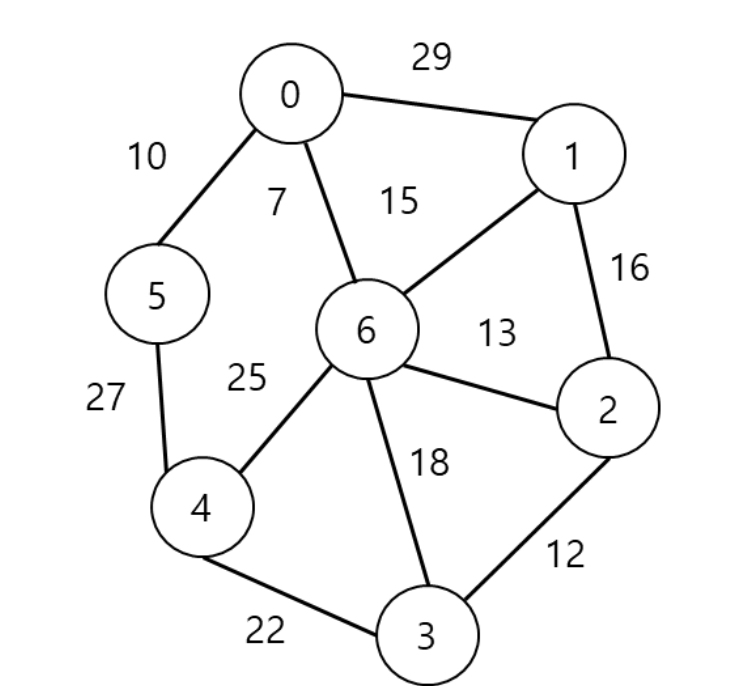
위와 같은 가중치 그래프가 존재한다고 하자.
우선 , 시작 정점을 정해야한다. 0을 시작 정점으로 정하자
0을 기준으로 간선이 연결된 정점은 5, 6, 1이다. 이 중에서 가중치가 7의 간선을 선택하여 정점 6로 이동한다.

여기서가 중요하다.
Prim 방법은 이동한 정점을 기준으로 또다시 작은 가중치를 탐색하는 게 아니라, 이동된 정점까지 합쳐서 위 그림의 트리를 기준으로 가중치가 작은 노드를 탐색한다.
정점 0에서 갈 수 있는 곳은 5, 1이고 정점 6에서 갈 수 있는 곳은 1,2,3,4이다.
이 5개의 정점(1은 중복이므로) 중에서 연결된 간선의 가중치가 가장 적은 값은 정점 5이다. 가중치가 10으로 가장 작다.
그럼 0과 5를 또 연결한다.

이렇게 또 연결된 트리를 기준으로 갈 수 있는 길을 찾아 가중치가 가장 작은 값을 찾으면 된다.


최종적으로는 갈 수 있는 곳이 없게 될 것이다.
위 내용을 C언어 코드로 작성해보겠다.
인접행렬으로부터 Prim 수행
#include <stdio.h>
#include <limits.h>
#define V 5 // 정점의 개수
int minKey(int key[], int mstSet[]) {
int min = INT_MAX, min_index;
for (int v = 0; v < V; v++)
if (mstSet[v] == 0 && key[v] < min)
min = key[v], min_index = v;
return min_index;
}
void printMST(int parent[], int graph[V][V]) {
printf("Edge \tWeight\n");
for (int i = 1; i < V; i++)
printf("%d - %d \t%d \n", parent[i], i, graph[i][parent[i]]);
}
void primMST(int graph[V][V]) {
int parent[V]; // MST에 저장된 트리
int key[V]; // 최소 비용을 저장
int mstSet[V]; // MST에 포함 여부를 저장
for (int i = 0; i < V; i++)
key[i] = INT_MAX, mstSet[i] = 0;
key[0] = 0;
parent[0] = -1;
for (int count = 0; count < V - 1; count++) {
int u = minKey(key, mstSet);
mstSet[u] = 1;
for (int v = 0; v < V; v++)
if (graph[u][v] && mstSet[v] == 0 && graph[u][v] < key[v])
parent[v] = u, key[v] = graph[u][v];
}
printMST(parent, graph);
}
int main() {
int graph[V][V] = {
{0, 2, 0, 6, 0},
{2, 0, 3, 8, 5},
{0, 3, 0, 0, 7},
{6, 8, 0, 0, 9},
{0, 5, 7, 9, 0}};
primMST(graph);
return 0;
}
실행 결과

인접리스트로부터의 Prim 수행
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
#define V 5 // 정점의 개수
struct Node {
int dest;
int weight;
struct Node* next;
};
struct Graph {
struct Node* head[V];
};
struct Node* createNode(int dest, int weight) {
struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
newNode->dest = dest;
newNode->weight = weight;
newNode->next = NULL;
return newNode;
}
struct Graph* createGraph() {
struct Graph* graph = (struct Graph*)malloc(sizeof(struct Graph));
for (int i = 0; i < V; i++)
graph->head[i] = NULL;
return graph;
}
void addEdge(struct Graph* graph, int src, int dest, int weight) {
struct Node* newNode = createNode(dest, weight);
newNode->next = graph->head[src];
graph->head[src] = newNode;
newNode = createNode(src, weight);
newNode->next = graph->head[dest];
graph->head[dest] = newNode;
}
int minKey(int key[], int mstSet[]) {
int min = INT_MAX, min_index;
for (int v = 0; v < V; v++)
if (mstSet[v] == 0 && key[v] < min)
min = key[v], min_index = v;
return min_index;
}
void printMST(int parent[], int graph[V][V]) {
printf("Edge \tWeight\n");
for (int i = 1; i < V; i++)
printf("%d - %d \t%d \n", parent[i], i, graph[i][parent[i]]);
}
void primMST(struct Graph* graph) {
int parent[V]; // MST에 저장된 트리
int key[V]; // 최소 비용을 저장
int mstSet[V]; // MST에 포함 여부를 저장
for (int i = 0; i < V; i++)
key[i] = INT_MAX, mstSet[i] = 0;
key[0] = 0;
parent[0] = -1;
for (int count = 0; count < V - 1; count++) {
int u = minKey(key, mstSet);
mstSet[u] = 1;
struct Node* temp = graph->head[u];
while (temp != NULL) {
int v = temp->dest;
if (mstSet[v] == 0 && temp->weight < key[v]) {
parent[v] = u;
key[v] = temp->weight;
}
temp = temp->next;
}
}
printf("Edge \tWeight\n");
for (int i = 1; i < V; i++)
printf("%d - %d \t%d \n", parent[i], i, key[i]);
}
int main() {
struct Graph* graph = createGraph();
addEdge(graph, 0, 1, 2);
addEdge(graph, 0, 3, 6);
addEdge(graph, 1, 2, 3);
addEdge(graph, 1, 3, 8);
addEdge(graph, 1, 4, 5);
addEdge(graph, 2, 4, 7);
addEdge(graph, 3, 4, 9);
primMST(graph);
return 0;
}
실행 결과

'자료구조' 카테고리의 다른 글
| [자료구조] Dijkstra 알고리즘, 그래프의 최단 경로 찾기 (0) | 2024.08.21 |
|---|---|
| [자료구조] Kruskal 알고리즘 (0) | 2024.08.20 |
| [자료구조] 그래프(Graph), 인접 행렬, 인접 리스트 (0) | 2024.08.12 |
| [자료구조] 이진 탐색 트리(Binary Search Tree) (0) | 2024.08.12 |
| [자료구조] 이진트리(연결리스트), 전위순회, 중위순회, 후위순회 - C (0) | 2024.08.10 |





